Ejercicios Resueltos
PAGINA EN CONSTRUCCION
CALIDAD | CAPACIDAD | INVENTARIOS | LOCALIZACIÓN | M.R.P.| PERT- CPM | PLANEACION AGREGADA | PRODUCTIVIDAD | PROGRAMACION LINEAL |
CAPACIDAD
Respuestas a Problemas de Capacidad
1.1000 un/ año/ 0.80 x 0.75= 1667 unidades
2.Es necesario producir: 900 000/ 0.6 x 0.7 = 2 142 857 un.
1 máq. = 34 un./ mes; en 12 meses = 34 un./ mes x 12 meses = 408 un./ año
408 un. = 1 máq.
2 142 857 un. = 5252 máq.
Demanda anual (D) = 12000 un.
Costo de mantener/un./año (i * C) = $ 1
Costo de ordenar (S) = 15 $/un
Tiempo de entrega = 5 días
Existencia de seguridad: 200
Precio unitario: $ 0.10
Respuestas a Problemas de Inventarios
1.
Q opt = Ö(2* $ 15 * 12000 un )/ ($ 1 $/un)
Q opt = 600 un.
CT = C * D + S * D/Q + i C Q/2 + (i * C) *Inv. Seg.= $ 0.10 * 12000 + $ 15 * 12000/ 600 + $ 1 * 600/2 + $ 1 * 200
CT = $ 2000
Se pide:
a) Determinar la productividad analizada desde el valor de la producción durante dicha semana.
b) ¿De qué otros modos podría ser analizada la productividad? ¿Usted qué piensa de ello?
c) ¿Cuál ha sido el rendimiento de la capacidad?
Respuestas a Problemas de Productividad
1.
a) Vtas: = 410 u * 48 + 2490 u * 120 = $318480
Insumo = 105 * 40 = 4200 hh;
Productividad = 75,83 $/hh
b) También 318 480/ 105 operarios ó 2900/ 105 * 40 (ambas de menor jerarquía que la de a))
c) 2490/2900 = 85,86%
El departamento de rayos X de un hospital tiene dos máquinas, A y B, que pueden utilizarse para revelar fotografías. La capacidad máxima de procesamiento diaria de estas máquinas es A = 80 y B = 100 radiografías. El departamento debe planear procesar al menos 150 radiografías por día. Los costos de operación por radiografía son $ 4 para la máquina A y $ 3 para la máquina B. ¿Cuántas radiografías por día debe procesar cada máquina para minimizar costos?
Resolver el problema gráfica y analíticamente.
¿Cuánto está dispuesto a pagar por capacidad adicional en la máquina A?
Respuestas a Problemas de Programación Lineal
1.
I. Resolución gráfica y analítica:
Z = 4 A + 3 B = mínimo
(1) A < ó = 80
(2) B < ó = 100
(3) A + B > ó = 150
Para graficar la recta de isocostos:
4 A + 3 B = 120 Þ A = 0; B = 40 y B = 0; A = 30
Llevando esta recta en forma paralela hasta tocar el primer punto de la gráfica (punto más cercano al origen es el de menor costo), se encuentra que la combinación óptima es la correspondiente al punto (a).
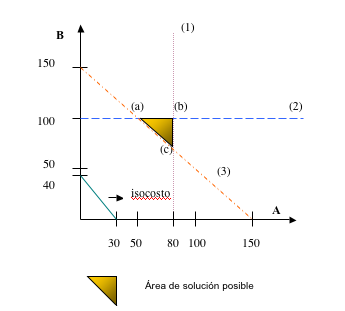
Para verificar que (a) es la mezcla que minimiza costos, reemplazamos los valores que toman A y B en los puntos (a), (b) y (c) en Z:
Þ A = 50
Z (a) = 4 * 50 + 3 * 100
Z (a) = $ 500
Z (b) = 4 * 80 + 3 * 100
Z (b) = $ 620
Þ B = 70
Z (b) = 4 * 80 + 3 * 70
Z (b) = $ 530
II.¿Cuánto está dispuesto a pagar por capacidad adicional en la máquina A?
No pagaría nada por capacidad adicional en dicha máquina, ya que hay capacidad suficiente (de las 80 radiografías diarias que puede procesar, la mezcla óptima es realizar 50) - y, por otra parte, sus costos de operación son más altos que los de la máquina B -.
Página de Inicio | Página Anterior | Artículos y Documentos | Casos y Minicasos | Otros Recursos |
Universidad Nacional de Luján
Int. Ruta 5 y 7 - 6700 Luján - República Argentina.